Как работают нейросети Простое объяснение в картинках

Нейросеть — ​это компьютерная программа, способная к обучению. Перед ней можно поставить практически любую задачу. И если сперва показать машине тысячу-другую верных решений, то затем она научится находить правильный ответ самостоятельно. За нейронными сетями стоит сложная математика, при этом модель компьютерной сети построена по принципу работы нервных клеток человека, то есть биологических нейронных сетей. В общем всю эту математику проще всего объяснить в картинках.

Непростое человеческое

Контекст и опыт

Перед вами десять картинок. Человек без труда узнает на всех десяти цифру 6. Для машины же это набор совершенно разных изображений, никак не связанных между собой. Что помогает человеку узнать «шестерку»? Контекст и опыт.

Контекст помогает нам разобрать даже почерк врача: если на месте буквы появляется странный крестик, мы понимаем, что это, видимо, «т» или «к». К сожалению, компьютеры на сегодняшний день мало что смыслят в контексте. Зато опыта они набираются гораздо быстрее людей. Покажите нейронной сети тысячу рукописных цифр, и она научится их различать.

На месте цифр может быть что угодно: кошки, лица, раковые опухоли. Речь идет не обязательно об изображениях: обучить программу можно на биржевых сводках, художественных текстах, аудиозаписях — ​любых оцифрованных данных. Но прежде, чем обучать, давайте разберемся с матчастью — какие виды структур нейронных сетей существуют.

Виды структур нейросетей

Нейронные сети прямого распространения или FFNN (от английского Feed Forward Neural Networks) имеют две входные клетки и всего одну выходную. Обучение осуществляется по принципу обратного распространения ошибки между вводом и выводом, что предполагает способность сети моделировать связь между входными и выходными слоями, генерируя определенный результат. FFNN применяются для распознавания речи, письменных символов, изображений и компьютерного зрения.

Сети радиально-базисныx функций (RBFN, radial basis function network) обладают такой же структурой, что и предыдущие с той лишь разницей, что для активации применяется радиально-базисная функция. Эта ИНС (искусственная нейронная сеть) находит применение для решения задач аппроксимации, а также классификации и прогноза временных рядов.

Нейронная сеть Хопфилда (HN, Hopfield network) характеризуется симметрией матрицы образующихся связей. Это означает, что смещение, вернее вход и выход данных осуществляется в рамках одного и того же узла. Эта нейронная сеть также имеет название сеть с ассоциативной памятью — в процессе обучения она запоминает определенные шаблоны и впоследствии возвращается к одному из них.

Автоэнкодер (Autoencoder) — сеть прямого распространения, которая умеет восстанавливать входные данные на узле выхода. Подобная структура применяется для классификации данных, сжатия и восстановления информации.

Свёрточные нейронные сети (CNN, convolutional neural networks) основное применение нашли в области распознания изображений. Технология их работы заключается в том, что она считывает изображения небольшими квадратами, потом передает информацию через сверточные слои. Логичным продолжением операции становится подключение FFNN, которые выдают определенный результат на основе полученных данных (так сверточные нейронные сети становятся глубинными). Если на обрабатываемых картинках изображена мышь, то сети констатируют этот факт.

Развёртывающие нейронные сети (DN, deconvolutional networks), как следует из их названия, обладают обратным к CNN действием. Для примера обратимся к помощи уже взятой выше мыши. Если нужно, наоборот, создать или найти картинки с изображением грызуна, для запуска функции активации DN достаточно одного этого слова, вернее, определённого бинарного вектора.

Генеративно-состязательные сети (GAN, Generative Adversarial Network) используются для досконального копирования цифровых данных, например, изображений. Применение GAN нашли в области кибербезопасности. А еще с их помощью можно наложить на фото эффект старения.

Квадратно-гнездовое

Сенсорный слой

Приступим к строительству и обучению нейронных сетей. Разделим изображение на точки (пиксели): 30 по вертикали и 30 по горизонтали. Каждый из пикселей имеет свою яркость. Пусть черные пиксели имеют значение 0, белые — ​1, а градации серого дают дробные значения, например 0,4 или 0,8. Эти 900 пикселей — ​наши первые нейроны, точнее нейроны входного слоя, или сенсоры.

Псевдоживое многослойное

Структура нейросети

Наша нейросеть будет состоять из входного, выходного и двух промежуточных (скрытых) слоев. Входной слой воспринимает рукописные цифры и состоит из 900 нейронов. Выходной слой выдает один из десяти возможных результатов: числа от 0 до 9. Поэтому нейронов в нем будет 10, они называются реагирующими. Промежуточные слои имеют по 15 нейронов, их элементы называются ассоциативными.

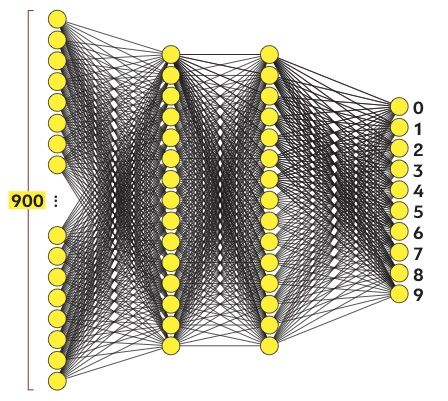
Концептуально нейроны имитируют клетки живого мозга. Как и для настоящих нейронов, для компьютерных тоже важны связи. Каждый нейрон связан со всеми нейронами соседнего слоя.

Тайное искомое

Связи и веса

Посмотрим на первый нейрон промежуточного слоя (назовем его b1). Он связан с каждым из 900 нейронов входного слоя (назовем их a1 — ​a900). Собственно, нейрон b1 — ​это математичес­кая формула, длинная, но довольно простая. Она показывает, насколько сильно каждый из сенсоров a1 — ​a900 влияет на значение b1.

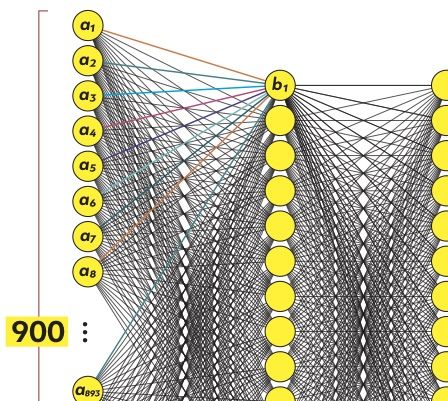
На рисунке связи нейрона b1 имеют разные цвета, чтобы показать: каждый нейрон входящего слоя имеет свой коэффициент, или вес, в общей формуле b1. Эти веса, настроенные оптимальным образом, — ​вот то тайное знание, которое является результатом глубокого машинного обучения.

Абстрактное обобщенное

Ассоциативные слои

Итак, процесс машинного обучения направлен на то, чтобы придать всем связям внутри искусственной нейронной сети оптимальные веса. Для чего нужны промежуточные слои? Выражаясь очень образно, они помогают машине обобщить накопленный опыт. Проведем мысленный эксперимент. Как мы, люди, узнаем шестерку? Она состоит из кружочка и «хвостика» слева вверху.

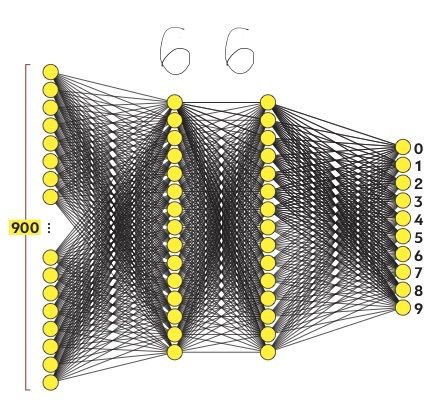
Представим, что предпоследний (второй скрытый) слой нейронной сети разбирается во взаимном расположении кружочков, «хвостиков» и «крючочков», из которых состоят цифры. А первый скрытый слой умеет выделять на картинке сами кружочки и «хвостики» по сочетанию пикселей. Если бы речь шла о человеческой логике, то скрытые слои представляли бы собой разные уровни абстракции и обобщения.

Горящее пороговое

Активация нейронов

Запустим нашу нейросеть: расставим веса в произвольном порядке, покажем сенсорам шестерку и посмотрим, какой из выходных нейронов активируется. Под активацией подразумевается превышение некоего порогового значения. Например, если формула нейрона выдает результат больше 0,8, то он «загорается», или активируется.

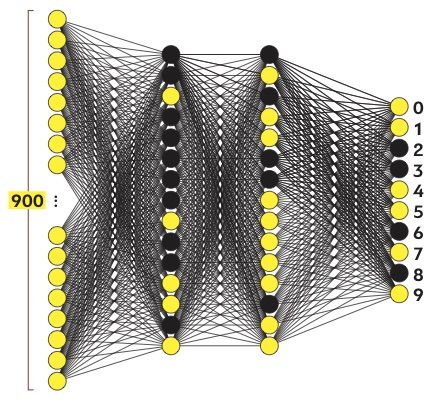
Вполне вероятно, что при первом запуске «загорелось» несколько реагирующих нейронов. Машина «признала» в шестерке и 8, и 2, и 3, и все эти результаты не имеют никакого отношения к истине. Нейросеть еще предстоит обучить.

Остроумное реверсивное

Обратное распространение ошибки

Если бы вес каждой связи искали простым перебором, процесс занял бы вечность. Сокращает путь главное ноу-хау машинного обучения — ​алгоритм обратного распространения ошибки. Метод обратного распространения позволяет нейронной сети, словно находчивому школьнику, подогнать значения переменных в уравнении, зная правильный ответ.

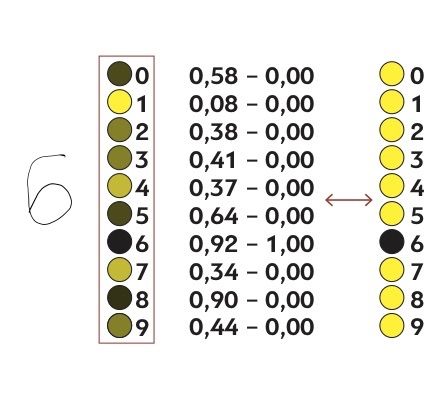
Посмотрим, насколько полученный в первой итерации результат отличается от желаемого. Допустим, нейрон, обозначающий единицу, получил значение 0,08. Это мало, как и должно быть, ведь на входе не единица. Значит, веса для связей, подключенных к этому нейрону, нужно скорректировать совсем немного. А вот нейрон, отвечающий за восьмерку, «загорелся» и показал результат 0,9. Это никуда не годится: восьмерка не шестерка. Значит, связи этого нейрона нуждаются в сильной коррекции.

Теплое быстрое

Градиентный спуск

Говоря чуть более математическим языком, каждый набор нейронов есть функция от множества переменных — ​весов нейронов, стоящих за ним. Для одного выходного нейрона — того, что отвечает за шестерку, — нам нужно найти максимум этой функции. Для всех остальных — ​минимумы.

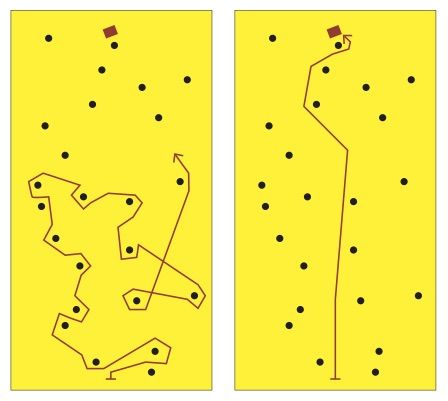
Представьте, что вам нужно найти кошелек, потерявшийся в лесу. Методично прочесать весь лес — ​практически невыполнимая задача. Но если что-то подсказывает вам направление движения и оставшееся расстояние до кошелька, найти его будет намного проще. Вы сперва разгонитесь до высокой скорости, а подойдя ближе к искомому объекту, замедлитесь и поищете внимательнее. Такая технология поиска в математике называется градиентным спуском. А маячок, на который вы ориентируетесь, появляется благодаря алгоритму обратного распространения ошибки.

Среднее разнообразное

Обучение на датасетах

Посчитав, насколько сильно значения всех нейронов отличаются от желаемых, мы получим суммарную ошибку сети. Найти ее минимум было бы достаточно, если бы мы хотели научить такую сеть отличать шестерку от других цифр. Чтобы машина могла распознавать любую цифру, нужно каждый раз демонстрировать ей датасет (набор data, то есть данных) из десяти цифр и стремиться свести к минимуму среднюю ошибку для всех десяти. Сложность задачи возводится в десятую степень.

Чтобы нейросеть научилась распознавать цифры, написанные разным почерком, нужно продемонстрировать ей множество рукописных цифровых комплектов. И проделать множество вычислений, чтобы найти оптимальные средние значения для всех весов. Это ресурсоемкая задача — как по вычислительной мощности, так и в плане подготовки огромного датасета. Но результат того стоит.

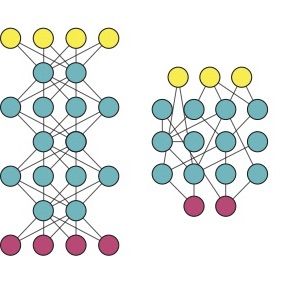
Неизвестное машинное

Неразумная математика

Помните разговор о кружочках и «хвостиках»? Компьютер позволяет визуализировать происходящее на скрытых уровнях нейронной сети, чтобы увидеть… что никаких кружочков там нет. Абстракция и обобщение — ​человеческие понятия. Нейросеть «мыслит», точнее сказать, работает совершенно по-другому. Это просто математика, а вовсе не разум.

Если показать нашей нейронной сети, скажем, фотографию кота, она с уверенностью скажет, что это три, пять или девять. Для нее весь мир состоит только из цифр, и никакой иной контекст ей неведом.

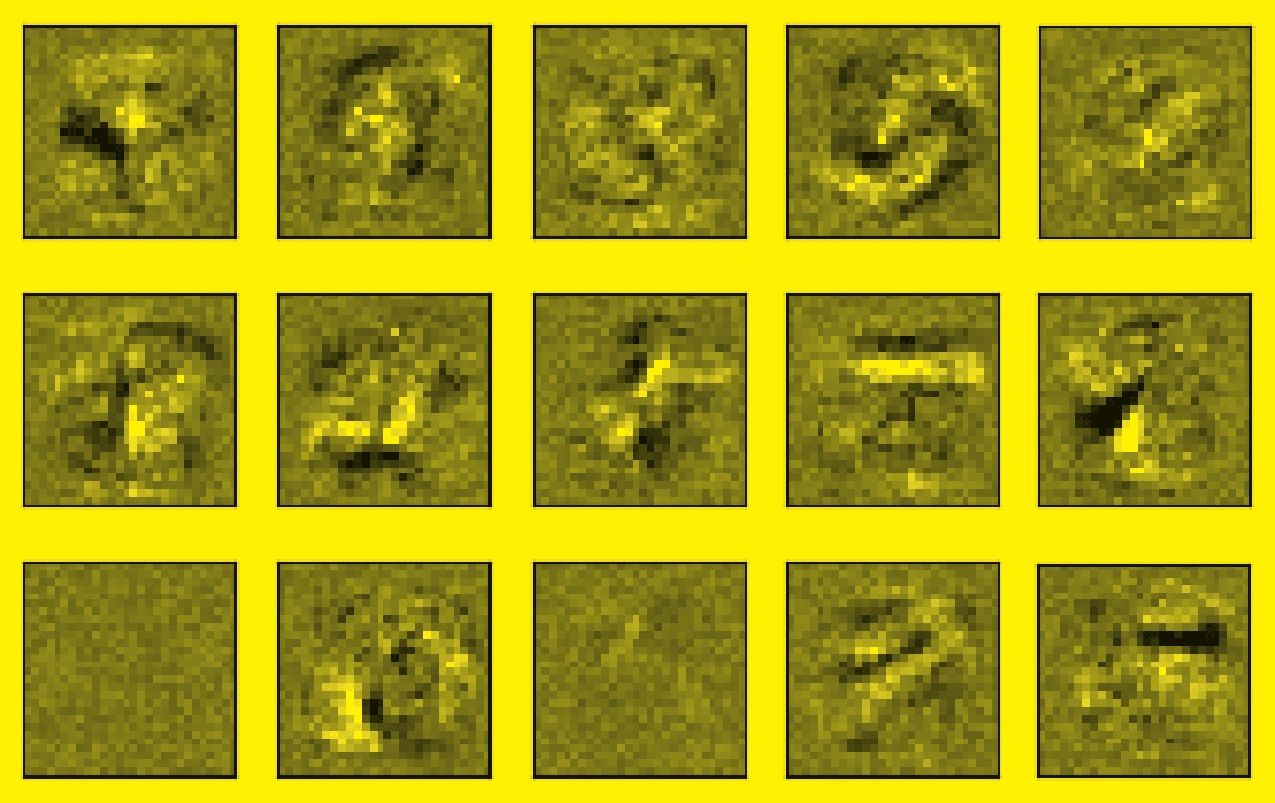
Наше журнальное объяснение нейронной сети упрощено до предела, а структура давно устарела — ​таким машинное обучение было в 1960-е. Современным специалистам приходится иметь дело с десятками и сотнями всевозможных параметров, не только весами и количеством слоев. И чем совершеннее становится искусственный интеллект, тем сложнее нам становится понять, что творится глубоко в его «мыслях».

Читайте также максимально простое объяснение, как работает блокчейн: